"Jugend Forscht" Arbeit aus dem Jahr 1992

Der Bau des 'CD-Spektrographs'

Vorwort:

Aus softwaretechnischen Gründen müßen wir Lambda (Wellenlänge ) als Γ darstellen. Wir hoffen, daß dies nicht zu sehr stört.

Die Bilder entnehmen Sie alle dem Anhang.

Idee

Im letzten Jahr zeigte unser Mitschüler Andreas Goris, daß man mittels einer CD weißes Licht, wie mit einem Prisma oder einem Gitter, in seine Spektralfarben zerlegen kann (Die CD arbeitet hier als Spiegelgitter). Dadurch angeregt beschlossen wir ein 'CD-Spektroskop' zu bauen, welches quantitative Messungen erlaubt. Dazu mußte als erstes die Gitterkonstante der CD bestimmt werden. Wir benutzten dazu einen Laser, da er monochromatisches und nahezu punktförmiges Licht liefert.

Was ist ein Gitter

Ein Optisches Gitter ist eine Lichtdurchlässige Glas oder Plexiglasscheibe, die durch viele kleine Kratzer oder Verunreinigungen Stegweise Lichtundurchlässig. Diese Kratzer sind genauso breit wie die Lichtdurchlässigen Stege. Dies sieht dann stark vergrößert so aus: ▮ ▮ ▮ ▮ ▮ Die Anzahl der Kratzer pro mm ist die Gitterzahl (hier 653 Linien pro mm). Zieht man aus der Gitterzahl den Kehrwert erhält man die Gitterkonstane (g_k), mit der man erst die verschiedenen Formeln berechnen kann. Die CD hat durch ihre digitale Aufzeichnungsweise, die nur Nullen und Einsen kennt, bedingt genauso wie ein Gitter durchlässige und undurchlässige Stege der gleichen Breite. Diese sind zwar nicht ganz regelmäßig, aber dies hat keine / kaum negative Auswirkungen auf die Funktionsweise. Der einzige Unterschied zwischen der CD und einem Gitter ist, daß die CD die gebrochenen Lichtstrahlen reflektiert, und nicht wie ein Gitter durchläßt.

Die Gitterkonstante der CD

Wie in Bild 1 gezeigt, richteten wir (unter Aufsicht von Herrn Stein) den Laserstrahl auf die CD. Über

ermittelten wir den Beugungswinkel α_k. Mittels der Gleichung für das Gitter

konnten wir nun die Gitterkonstante g berechnen, da λ = 632,8 nm und k= 1 (Spektrum der 1. Ordnung) bekannt waren.

Der Aufbau

Unser CD-Spektroskop sollte nicht zu unhandlich sein. Aus diesem Grund legten wir fest, daß das Spektrum im Bereich von 400 bis 800 nm auf eine Strecke von 16 cm abgebildet wird (2,5 nm pro mm). Daraus ergab sich eine Spektroskopgröße von..cm*.cm (Siehe folgende Rechnung und Abbildung).

Kostenvergleich

Ein Reflekionsgitter mit einer Auflösung von 100 Linien pro Millimeter kostet zum Beispiel bei LEYBOLD 243.- DM. Ein CD Stück mit einer durchschnittlichen Auflösung 500 - 600 Linien pro Millimeter kostet ungefähr 10.- DM. Das heißt, daß die CD bei einer 5 - 6 mal so guten Auflösung nur ≈ 1/24igstel eines Markengitters kostet.

Die Technik

Die Fotodiode

Um die Intensität des Spektrums in Abhängigkeit der Wellenlänge mittels eines Schreibers oder Computers aufzeichnen zu können, informierten wir uns über die technischen Eigenschaften von Fotowiderständen und Fotodioden. Wir entschieden uns für die Fotodiode BPX 63 da sie eine lichtempfindliche Fläche von nur 1 mm² besitzt, außerdem hängt der Fotostrom nahezu linear von der Beleuchtungsstärke E (in Lux) ab (siene Bild 5). Da die Empfindlichkeit S (in %) der Fotodiode aber auch von der Wellenlänge λ des Lichtes abhängt müßen die Angaben des Bildes 6 bei der Auswertung der Spektren berücksichtigt werden.

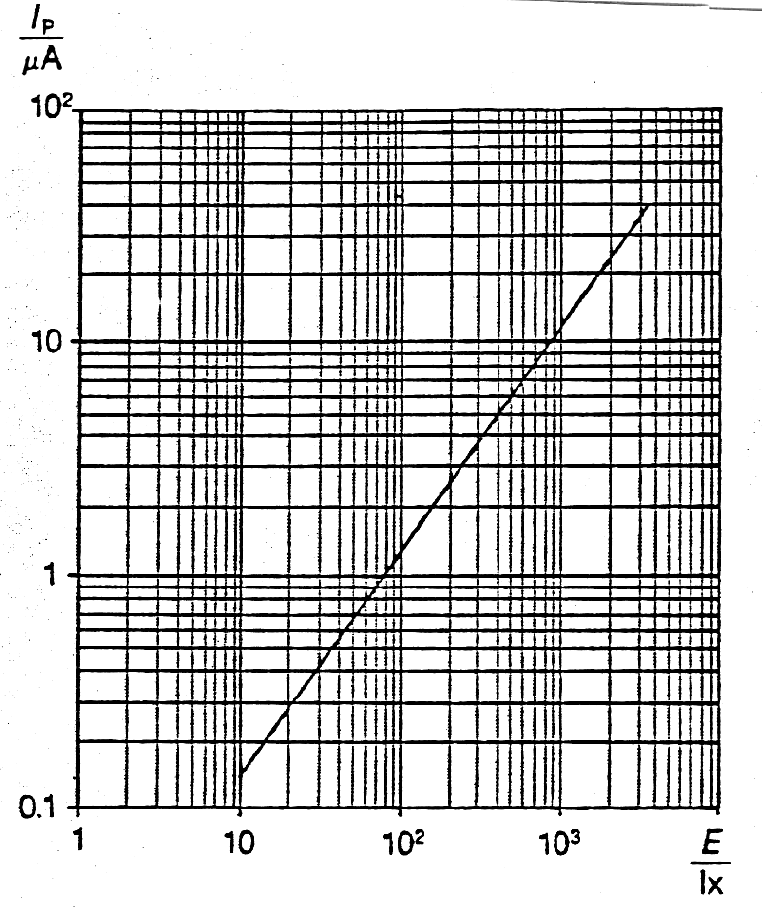Bild 5: Abhängigkeit des Fotostroms von der Beleuchtungsstärke E

Bild 6: Abhängigkeit der Empfindlichkeit S von der Wellenlänge

Führung der Fotodiode

Die Fotodiode sitzt auf einem aus FISCHER-TECHNIK gebautem Wagen, der von einer Gewindestange der Größe M4 angetrieben wird und von zwei weiteren Gewindestangen geführt wird. Die Gewindestange mit einer Länge von 16 cm wird von einem Schrittmotor angetrieben. Dies erschien uns als die beste Lösung, da die Gewindestange eine sehr genaue Positionierung des Wagens zuläßt.

Die Verstärkung

Zum Verstärken der von der Fotodiode gelieferten Signale benutzten wir den Operationsverstärker LF 356. Der bipolare FET - Eingang (Feld-Effekt-Transistor) hat den Vorteil sehr hochohmig zu sein, wodurch ein geringer Eingangsfehlstrom erreicht wird. Der Verstärkungsfaktor kann über die Widerstände R₁, R₂ und R₃ um jeweils den Faktor 10 geändert werden. (Den Schaltplan entnehmen Sie bitte dem Anhang)

Die Steuerplatine

Einen Schrittmotor steuert man, indem man seine Anschlüsse umpolt. Will man den Schrittmotor mittels eines Computers ansteuern, So braucht man vier Ausgänge die im Wechsel sowohl positiv wie negativ sein müssen. Da dies etwas umständlich ist, wird dem Computer eine kleine Steuerschaltung nachgeschaltet, die das Umpolen und Umschalten der Anschlüsse für den Computer übernimmt. Diese Schaltung arbeitet mittels zweier Relais, wobei Re₁ für die Umpolung der Anschlüsse zuständig ist und Re₂ die Umschaltung der Anschlüsse übernimmt. Da die Relais einen etwas höheren Strom von I ≈ 50 - 100 mA benötigen, der Computer aber so gut wie kein Strom zur Verfügung stellt, wird vor die Relais ein Transistor (BD 139) vorgeschaltet. Die beiden Widerstände (R₁ und R₂) begrenzen den Basisstrom, so daß der Computer und die beiden Transistoren nicht zerstört werden. R₃ und R₄ dienen zur Begrenzung des Stromes für den Schrittmotor. (Den Schaltplan entnehmen Sie bitte dem Anhang).

Die Hard- / Software

Das Cap-CS2

Als Interface zwischen Computer und Fotodiode / Schrittmotor benutzten wir das CAP-CS52 (ab hier "CAP" genannt) von der Firma LEYBOLD da uns dies von der Schule zur Verfügung gestellt wird und für unsere Zwecke vollkommen ausreicht. Das CAP besitzt zwei A/D-Eingänge, zwei D/A-Ausgänge und ein Realaisausgang, sowie vier TTL-Eingänge und vier TTL-Ausgänge und zwei digitale Eingänge (Lichtschrankeneingang) die aber für uns unwichtig sind. An den A/D-Eingang (Analog/Digital) schloßen wir die Fotodiode, an den D/A-Ausgang legten wir R₁. da dies für jeden Schritt des Schrittmotors umgeschaltet werden muß. Der D/A-Ausgang ist so programmiert, daß er als Steuerspannung V = 3 Volt abgibt, welche dann über T₁ verstärkt wird und Re₁ ansteuert. Re₂ legten wir an den Relaisausgang, da Re₂ nur umgeschaltet werden muß, wenn man die Drehrichtung des Schrittmotors verändern will. Da die Schaltleistung des Realaisausgang des CAP sehr gering ist, wird der Steuerstrom, der durch den Relaisausgang fließt, über T₂ verstärkt, bevor er Re₂ schalet.

Das Programm

Das Steuerprogramm ist im TURBO-PASCAL 5.0 geschrieben, da uns die Unterroutienen zur Ansteuerung des CAP's nur für TURBO-PASCAL vorlagen. Das Programm mit integrierten Beschreibungen entnehmen Sie bitte dem Anhang.

Neue Überlegung

Als sich bei unserer Untersuchung herausstellte, daß das Spektrum durch Rotieren der CD um ihre eigene Achse bewegt werden kann, überlegten wir, daß man die Fotodiode fest installieren könnte und nur die CD mittels eines Schrittmotors mit einem sehr kleinem Schrittwinkel drehen könnte. Dies hat den Vorteil, daß man erstens das 'CD-Spekrtoskop' kleiner gestalten kann, da der Wagen, der die Fotodiode durch das Spekrtum fährt, wegfällt und nur noch ein einziger 'Lichtstrahl' aus dem Spektrum von der CD zur Fotodiode 'übertragen' werden muß. Diesen 'Lichtstrahl' kann man dann über Umlenkspiegel im Zick-Zack durch das Gehäuse des Spektroskops 'laufen' lassen, wodurch sich die Auflösung stark erhöht, aber die Abmessungen des Spektroskopens relativ klein bleiben. Ein möglicher mechanischer Aufbau befindet sich im Anhang.

Der Anhang

Das Programm

Berechnung von X

a_k= 16 cm (Schirmgröße)
x = ?
λ₁ = 400 nm (Untere gewünschte Wellenlänge)
λ₂ = 800 nm (Obere gewünschte Wellenlänge)
k = 1 (1. Maximum)
g_x = 0.0000015 (Gitterkonstante)

Berechnung der Gitterkonstante

(Diese Messung wurde an der Tafel, und nicht mit unserem CD-Spektroskop durchgeführt, deswegen weichen verschiedene Werte wie z.B. α_k von den oben genannten Werten ab, was aber keine Auswirkungen auf g hat)

Baupläne

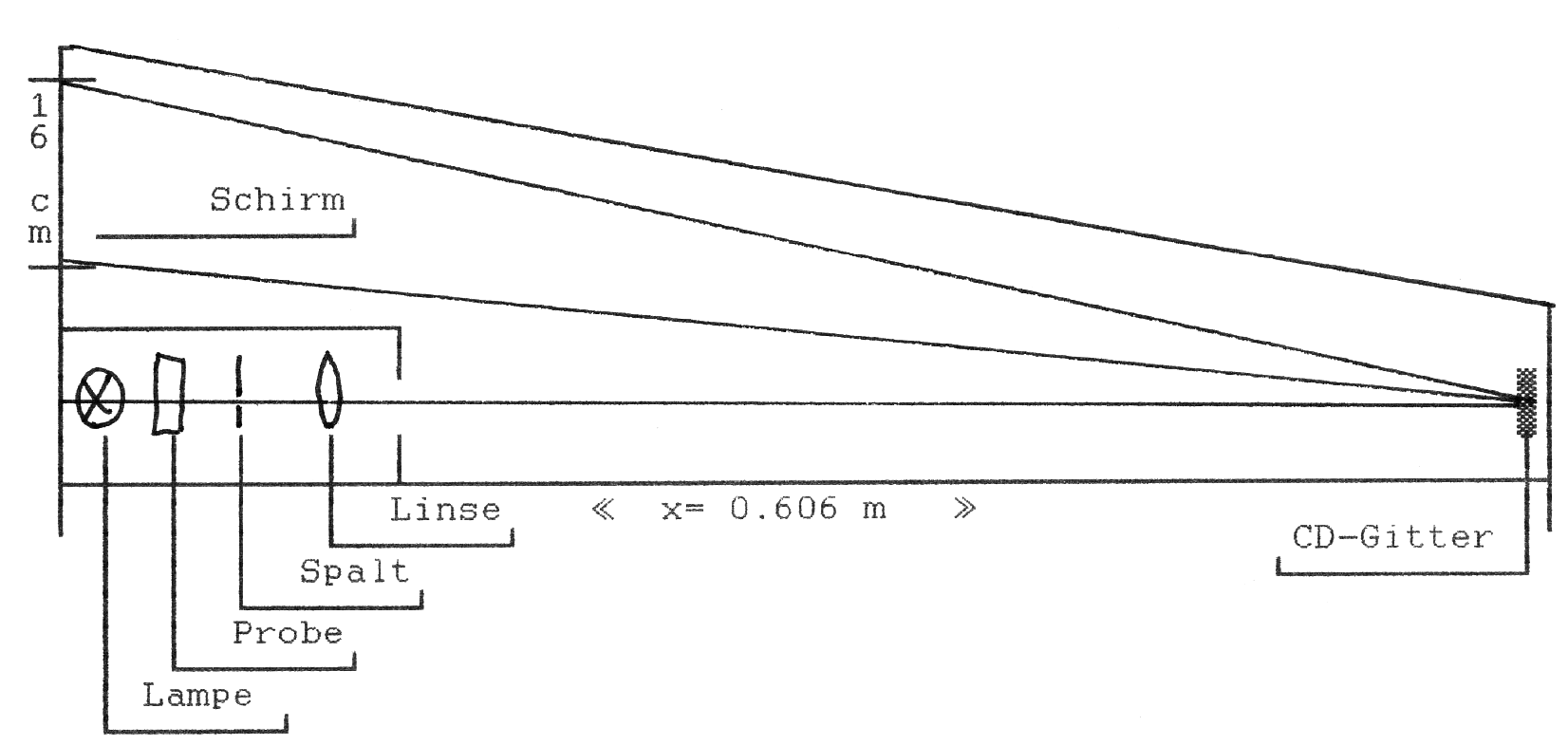Bild 4: Der mechanische Bauplan

Bild 5: Der mechanische Bauplan der Neuen Idee

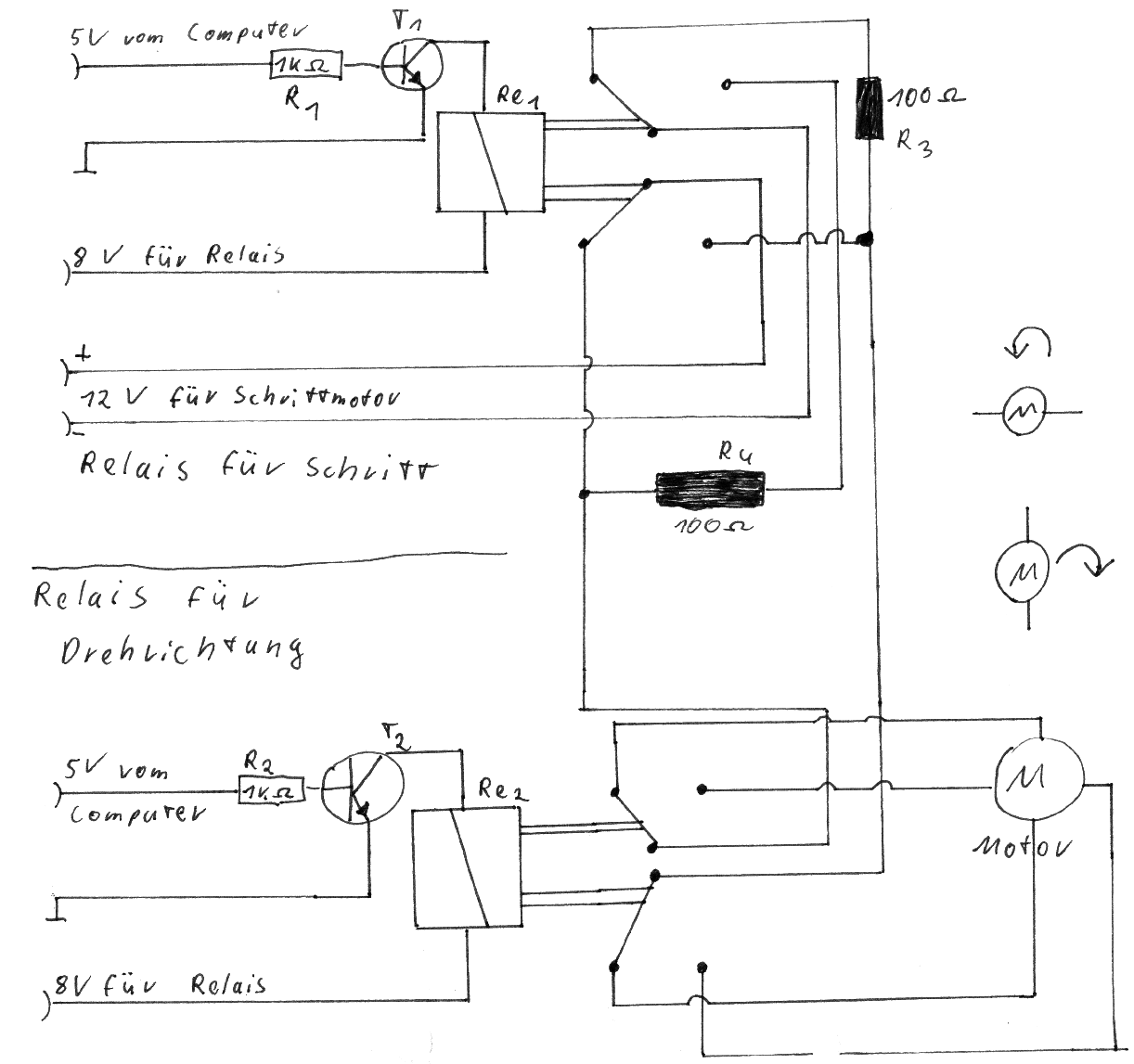Bild 7: Schaltplan der Steuerplatine

Literaturverzelchnis

1. 'Metzler Physik', J. Grehn (Hg.), 2. Auflage, J. B.Metzlersche Verlagsbuchhandlung Stuttgart, ISBN 3-476-50209-0
2. 'Praxis der Naturwissenschaften', Heft 3/40 « 15. April 1991, Artikel: "Bestimmung der Intensitätsverteilung bei einem optischen Spektrum", Autor: F. Wörlen, S 19-25, Aulius Verlag, Deubner & CO KG, Köln

Die orginal Arbeit als PDF

Titelbild © 2014 Evie Shaffer